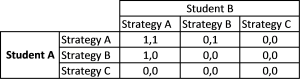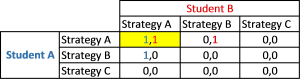Game Theory is the mathematical modelling of decision making processes. In simple terms, it uses mathematical expressions to analyse strategies employed by players in order to maximize their payoffs from the game. When applied in a social perspective, game theory can model individuals’ behaviours (strategies) in relation to the pursued benefit (payoff). In the context of Online Social Networks (OSNs), Game Theory is used to study user patterns in structural balance (inter-personal relations that have produced gains in the past), strategies for social decision problems and evolution of co-operation in dynamic environments.[1] Prediction of behaviour can be immensely valuable in the designing of an OSN. After all, Social Networks rely on user interaction to derive content. In the case of ‘LessonPlan’, user interaction is what will provide the added value on top of the initial information about the modules. Through module feedback, commentary on the practical aspects of teaching or coursework, students will be able to collaborate, solve problems, improve their performance and communicate necessary or desirable changes to the academics and the University. In other words, social interaction in the platform is essential for students to derive gains from it. Below we will consider the likelihood of random students to see this potential value of participating in the platform.

Even though Game Theory can be extensive and complex, for the purposes of this post we will examine how two concepts of Game Theory apply to ‘LessonPlan’. Namely, we will look at zero-sum games (or, more precisely, non-zero-sum) and Nash equilibria. To keep things simple, it is assumed that we are talking about a symmetric game (we are judging strategies and not who is employing them) and that synchronous updates are used (all players make their decisions at the same time). The assumption that there is complete information (all players know the strategies and payoffs beforehand) is also made.

Collaboration on ‘LessonPlan’ is a non-zero-sum game. In zero-sum games, a player can benefit only on the equal expense of others. Let’s consider module selection. Students take under consideration different criteria when choosing optional modules. For some students, course content (in terms of lectures’ material or engagement in class for example) is important. For others, important factors are the type or difficulty of the coursework or exam.

 

An example of a scenario could be like this:

Module X is optional. It involves philosophy of technology and the lecturer is encouraging students to discover related material on their own, which then gets used in the lectures. To compensate for how theoretical the module is, the coursework involves application of this theoretical knowledge on an innovative technical project that the students must build.

• Student A has a very technical background. He aims to become a successful computer engineer and, thus, would value the practical experience. He does not follow abstract theoretical concepts well, though, and as a result is unsure whether to choose the module or not.
• Student B is very good with social sciences, but struggles to grasp very technical concepts. He is very interested in the topics covered by the module, but the final assignment discourages him from selecting it.

Now, in regards to ‘LessonPlan’ we can have the following strategies:

• Strategy A: The student posts practical tips on the platform on how to best meet the requirements of the module
• Strategy B: The student does not post, but is a member of the platform and reads the content posted there
• Strategy C: The student does not use the platform at all

The payoffs for this game are to select and pass this module successfully.

If one of them submits tips on meeting the coursework requirements and the other only reads, the reader will have an easier time selecting the module and passing, now that he has advice on how to overcome his weaknesses. If neither of them posts, but both read, payoffs are going to be zero: they will equally be as unsure as they were at start. Notably, there is no scenario where they would need to sacrifice something. Now, if both of them post, both of them will be able to select the module and pass.

Now let’s consider the Nash equilibrium for the same scenario. In a Nash equilibrium the chosen strategy of each player is the one that benefits them the most while the strategies of the other players remain constant. In simple terms, the Nash equilibrium is the best choice a player can make while taking into account the decisions of the other players.

In the table above, best strategies for a student are highlighted in blue for Student A and red for Student B. Both students get the same gains if the other one posts and they either post or read. But, if they both read, none of them gains anything. Since the players are able to know each other’s decisions, it’s apparent that the best strategy is for both of them to post. It is the Nash equilibrium and highlighted in yellow.

 

 

---

[1] Van Segbroeck, S., et al. (2010). “Coevolution of cooperation, response to adverse social ties and network structure.” Games 1(3): 317-337.