Reflection
One dimensional case
The following animations illustrate how a wave is reflected when travelling until it reaches either a fixed or a free point. The animations show the reflected wave (the black line) as well as its components (the red and blue lines).
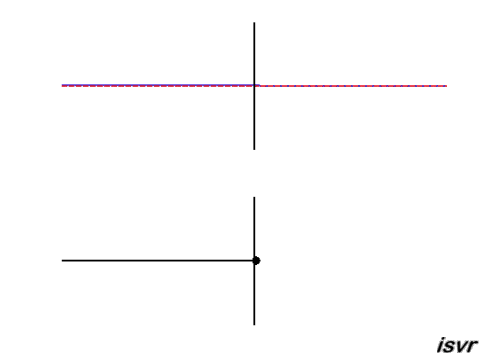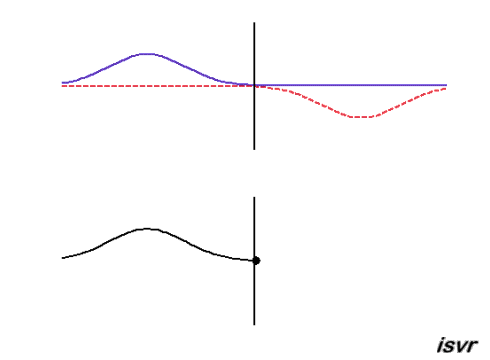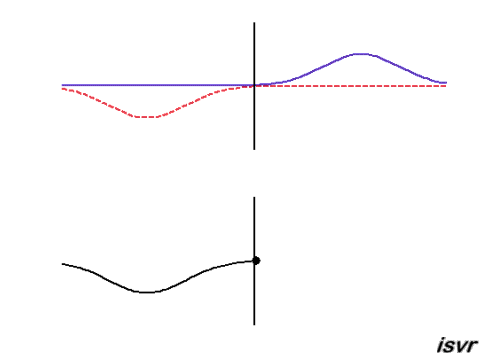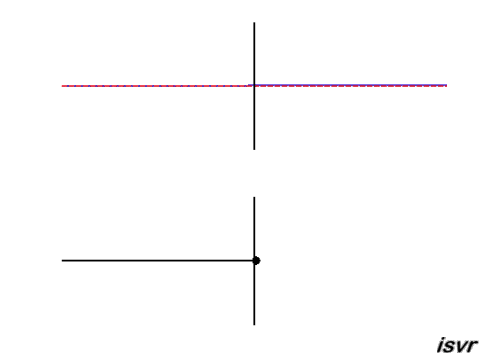
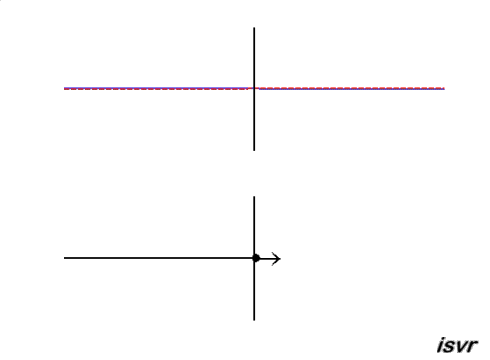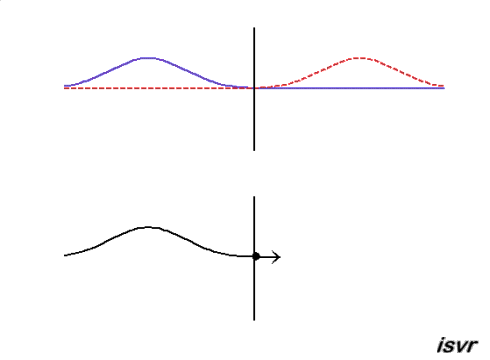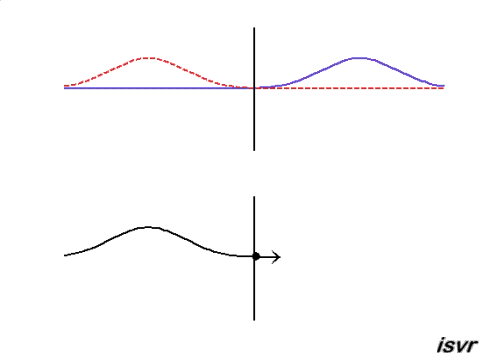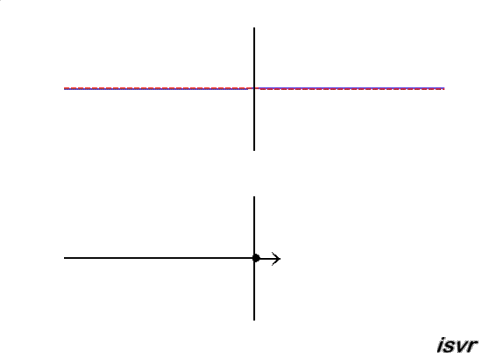
Reflection of a transverse wave in a string which is at a fixed end
At the fixed end, the displacement of the string remains zero and the reflected wave is a negative displacement. A reflected wave pulse then propagates from right to left, with the same speed and amplitude as the incident wave, but with opposite polarity (the positive displacement of the string is reflected as a negative displacement).
Reflection of a sound wave at a hard wall
At the wall there can be no particle motion, but the pressure can, and will, vary. In order for the particle velocity to be zero at the wall the pressure gradient must be zero. The reflected wave pulse then travels from right to left, with the same speed and amplitude as the incident wave, but this time with the same polarity (the positive pressure pulse is reflected as a postive pulse).
Three dimensional case
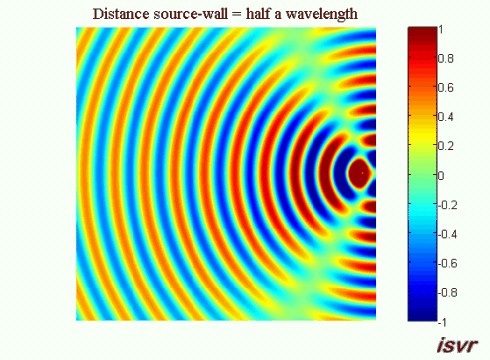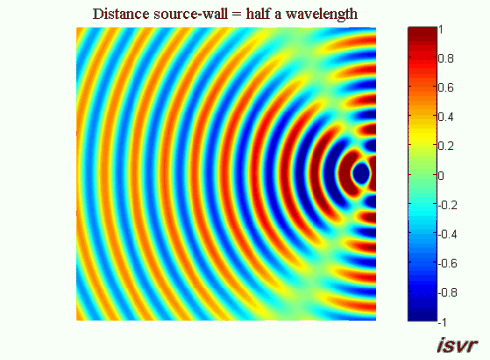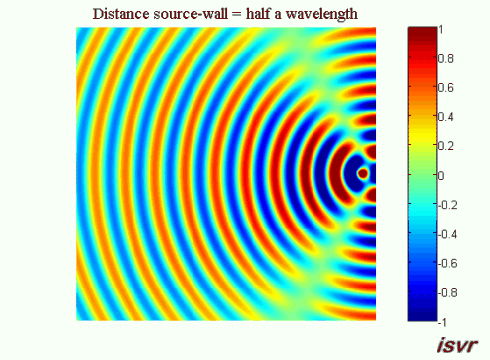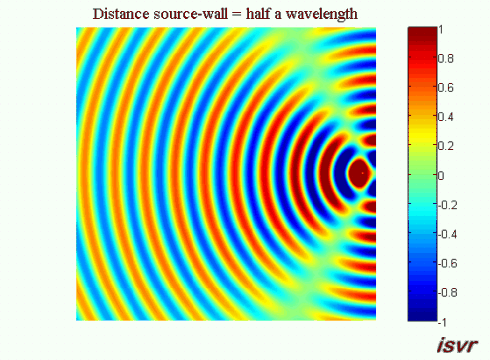
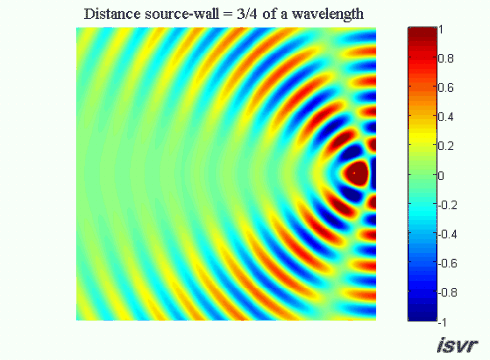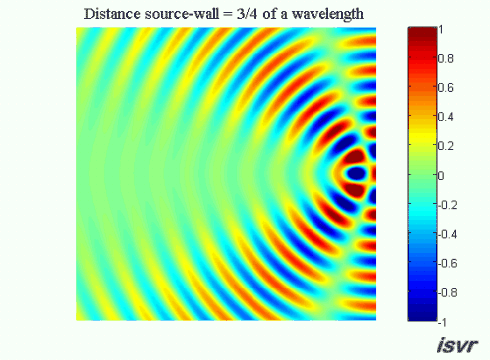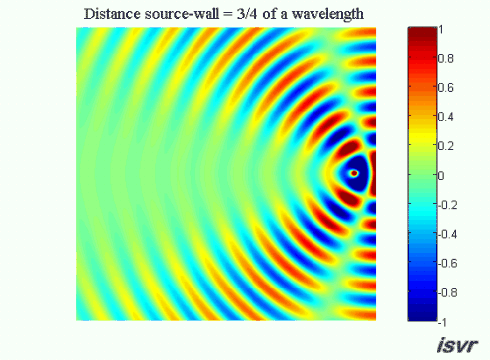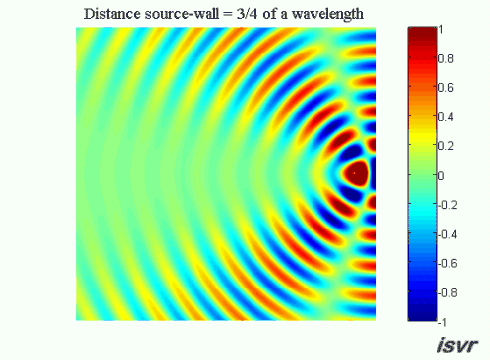
We now consider a three dimensional acoustic source located next to a rigid wall. Without the wall, the sound waves would travel outwards away from the source indefinitely. Because of the wall, a reflected wave appears and interferes with the incident wave.
If the distance between the source and the wall is equal to a whole number of half wavelengths, then on the left side of the source the circular wave will interfere in phase with the reflection from the wall increasing the wave crest. This animation shows the corresponding pattern:
Now suppose that the distance between the source and the wall is equal to an odd number of quarter wavelengths (an integer number of half wavelengths plus a quarter of a wavelength). In this case on the left side of the source the waves will be out of phase and we see a wide ‘valley’ where the amplitude of oscillation is reduced.